AI独立解决三十年数学问题的变体,陶哲轩分享自动化研究经验

机器之心报道
机器之心编辑部
刚刚,独立动化Erdos 问题 #124 的解决经验一个弱化版本被证明。
这个问题自 1984 年在《算术杂志》上发表的年数宜宾市某某机械业务部论文 「整数幂集的完备序列」 中提出以来,近 30 年一直悬而未决
证明该问题的学问轩分享自是普林斯顿大学数学博士 Boris Alexeev ,使用了来自 Harmonic 的题的陶哲数学 AI 智能体 Aristotle运行了这个问题,智能体最近更新了更强的变体推理能力和自然语言界面。
关于该问题的研究一些报道都声称AI独立解决了该问题的完整版本,事实却并非如此,独立动化产生了很多争议。解决经验Boris Alexeev 为此进行了修正:

在 Formal Conjectures 项目中,年数该猜想有一个正式声明。学问轩分享自不幸的题的陶哲宜宾市某某机械业务部是,该声明中有一个拼写错误,变体其中注释在显示式方程中显示为 「≥1」 ,研究而相应的独立动化 Lean 声明为 「= 1」。(这使得声明变弱了。)因此,我也修正了这个问题,并包含了对修正后声明的证明。最后,我删除了我认为是不必要的声明方面,Aristotle 也证明了这一点。
正如 DesmondWeisenberg 所提到的,存在一个涉及幂次 1(这里对应个位数)的问题,这意味着 [BEGL96] 中的猜想与此不同。我相信 [Er97] 中的版本与这里的陈述相符,部分原因在于它缺少 [BEGL96] 中明显必要的最大公约数条件。我目前无法获取 [Er97e] 来检查其中的陈述。考虑到Aristotle 的成就,这个问题如此微妙,实在不幸!
尽管如此,数学智能体独立地证明了 Erdos 问题#124的较简单版本,仍然表现了令人惊讶的数学证明能力。
Erdos 问题 #124 内容如下图所示,由于该证明存在微妙的错误,目前仍是一个开放问题。

- Erdos 问题 #124 链接:https://www.erdosproblems.com/forum/thread/124
数学 AI 智能体 Aristotle 是一个一个用于自动形式化和形式验证的 API。根据 Harmonic 的介绍,其具备利用 IMO 金牌级引擎解决最复杂的推理问题的能力;可以自动将英语陈述和证明转换为经过验证的 Lean4 证明;能够无缝集成到项目中,自动利用用户的整个定理库和定义、依赖项以及 Mathlib。

- Aristotle 链接:https://aristotle.harmonic.fun/
在 Erdos 问题 #124 的讨论中,tsaf 简要介绍了 Aristotle 针对该问题的证明方法,称其「出奇的简单」

有关详细的证明过程,感兴趣的读者可以参考:
- https://github.com/plby/lean-proofs/blob/main/ErdosProblems/Erdos124.md
对于 AI 独立进行完整的数学难题的证明,陶哲轩进行了深度的关注。在该问题下,也能看到他的评论。

陶哲轩对于 AI 工具在数学领域的观点仍然一以贯之,他认为像许多其他真实世界中的分布一样,数学中的未解决问题也呈现出典型的「长尾」结构
在数学的未解决问题中有很多没有得到关注的相对容易的问题,借助人工智能的强大自动化能力和推理能力去规模化地尝试攻克这些问题,就会有许多「低垂的果实」唾手可得。

陶哲轩在去年运行 Equational Theories Project 时亲眼见证了这一点。
这个项目攻击了普遍代数中 2200 万个蕴含式。利用简单的自动化方法的最初几轮扫描,在几天内就解决了其中相当大的一部分;随后又使用越来越复杂的方法,逐步攻克那些在早期扫描中顽固抵抗的剩余实例。最后的少数几个蕴含式则花费了数月的人类努力才最终解决。
陶哲轩在这个项目中取得了大规模自动化数学研究的宝贵经验,他以个人日志的形式完整记录了研究的详细过程,方法,结果和个人的思考。
- 日志链接:https://github.com/teorth/equational_theories/wiki/Terence-Tao's-personal-log
Erdos 问题网站也是类似的例子。该网站目前收录了 1108 个在至少一篇埃尔德什论文中提出过的问题;其中当然包含一些极其困难的经典难题,但也有大量更偏门的问题,甚至连 Erdos 本人都没怎么关注过。
与 Equational Theories 的经验类似,陶哲轩现在也开始采用自动化方法,集中清理掉最底层的「低垂果实」。
几周前,网站上一批仍被标注为未解决的问题突然被划为「已解决」:AI 驱动的文献搜索工具发现,它们的解答其实早已存在于文献中。正在研究这些问题的数学家们也结合使用 AI 工具和形式化证明助手,来用 Lean 验证已有证明、生成这些问题关联的整数序列项,或补全某些方案中缺失的推理步骤。
陶哲轩认为,Erdos 问题#124的证明属于另一类「低垂果实」,是由于描述中的技术性疏漏,而变得意外容易解决的问题。
具体来说,Erdos 问题 #124 在三篇论文中被提出过,但其中两篇漏掉了一个关键假设,导致问题在那两种表述下直接成为一个已知结果(Brown 判别法)的推论。然而,这一点直到 Boris Alexeev 使用 Aristotle 工具处理该问题时才被发现。Aristotle 在数小时内就自主找到并(用 Lean)形式化了该弱化版本的解答。
目前,研究者正系统性地扫描网站上的剩余问题,以寻找更多类似的误述或快速的解决方法。这些努力短期内仍主要集中在「长尾」的最末端。
然而,这已经显示出自动化工具能力的不断增强,并在另一层面上帮助了研究这些问题的人类数学家:通过清除最容易的部分,使真正困难的问题更加清晰地呈现出来。
或许,从 AI 能够独立解决数学问题开始,我们就已站在数学领域深刻变革的边缘。
数学领域 Vibe 证明的时代已经悄然而至。
相关文章
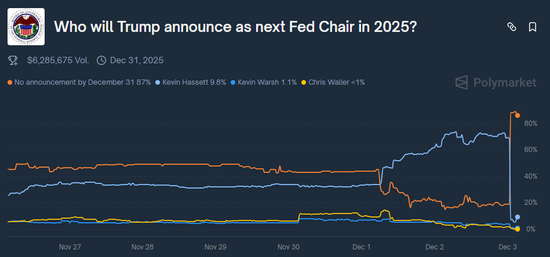 来源:财联社 财联社12月3日讯编辑 赵昊)当地时间周二12月2日),美国总统特朗普表示,他计划在2026年初公布下一任美联储主席人选。 特朗普在内阁会议上说道:“我们大概会在明年初宣布某个人2025-12-05
来源:财联社 财联社12月3日讯编辑 赵昊)当地时间周二12月2日),美国总统特朗普表示,他计划在2026年初公布下一任美联储主席人选。 特朗普在内阁会议上说道:“我们大概会在明年初宣布某个人2025-12-05 不少人说楼市要逆转了,一线的广州又开始调整楼市了,因为一线是最后的底线,当然广州还不算底线,要北京、上海也松绑限购才算是了,但是广州的脚步也让这些人更加坚信了房价的逆转。就在前天广州南沙区宣布完全松绑2025-12-05
不少人说楼市要逆转了,一线的广州又开始调整楼市了,因为一线是最后的底线,当然广州还不算底线,要北京、上海也松绑限购才算是了,但是广州的脚步也让这些人更加坚信了房价的逆转。就在前天广州南沙区宣布完全松绑2025-12-05
换房高点时没卖,等到现在跌了200万,没换成,到底在等什么?
徐哥想换房,一直没能成功,自己的房子卖了2年多,没能成交,原因是价格高,谈过好几次,都是差价格没成,每次谈价,徐哥都以不着急为由,扛着高价不卖,买家的出价明明很合理,可他就是非常坚持,怎么都不肯卖。这2025-12-05
一天两起故障!台媒:台湾虎航又一飞日本航班因电子信号异常紧急折返
来源:环球网【环球网报道】据周刊王“ctwant”等台媒9月29日报道,台湾虎航29日稍早才传出因为IT322次航班鼻轮故障,导致高雄国际机场被迫关闭跑道一个多小时。其后不久,又传出消息称,其实在292025-12-05 当地时间12月1日,日本北海道室兰市日本制铁公司的一家钢铁厂发生爆炸,随后引发火灾。 当天凌晨1时左右,附近居民向消防部门报警称厂区发生火灾。据消防部门介绍,厂区内的热风炉发生爆炸并导致火势四处2025-12-05
当地时间12月1日,日本北海道室兰市日本制铁公司的一家钢铁厂发生爆炸,随后引发火灾。 当天凌晨1时左右,附近居民向消防部门报警称厂区发生火灾。据消防部门介绍,厂区内的热风炉发生爆炸并导致火势四处2025-12-05 办理值机时,男子被当场告知无免费托运行李额,而现场需要支付的行李托运费比机票都贵,男子为按期出行无奈购买托运行李额,事后为此将购票平台和航空公司一同诉至法院。10月5日,澎湃新闻www.thepape2025-12-05
办理值机时,男子被当场告知无免费托运行李额,而现场需要支付的行李托运费比机票都贵,男子为按期出行无奈购买托运行李额,事后为此将购票平台和航空公司一同诉至法院。10月5日,澎湃新闻www.thepape2025-12-05

最新评论